论文主要提出了一种基于检索的时间序列预测方法。主要想解决在真实场景中,大部分的时间序列预测所能够获得的观测样本非常有限(如想要预测的时序长度占总时序的80%或以上),例如在智慧交通领域,预测传感器损耗的道路的交通情况,或者在环境监测领域,对某些环境恶劣、无法放置传感器的地点的温度变化情况。特别地,在工业场景中,也会存在基于少量的时序数据来预测未来许多天的场景,如广告行业中的流量预测、广告投放量估计等。
值得注意的是,本文使用的是关系检索,而非基于内容的检索,因为在输入时序数据很短的情况下,数据很可能是不够稳定的,从而导致检索到不可靠的时序片段。
论文的贡献主要有以下三个方面:
- 文章从条件熵的角度量化了时序预测的不确定性,并且论证了在拥有相似参考时序片段的情况下,会让模型更加轻松地学习到时序的模式;
- 文章提出了一个用于时序预测的两阶段算法ReTime,由关系检索的内容合成两部分构成;该方法也能够简单地扩展到时空序列预测、或是时序插值场景中去;
- 文章用了两个真实世界的数据集里验证了ReTime算法的有效性。
引理与证明
由于论文的出发点是使用 检索相似片段 的方式来提升模型在观测量很少的时序预测问题中的效果,作者首先给出了一系列定义与引理,从信息论的角度论证了这么做的有效性。
在提出时序预测的形式化定义时,作者将其视为了一种特殊的时序插值问题。即:给定一个时间序列 $X\in R^{T\times v}$,其中$T$表示时间步长,$v$ 表示变量数量;这个序列伴随了一个与前者形状相同的掩码序列 $M\in \{0,1\}^{T\times v}$ ,表示对应位置时间步的数据是否可见。时间插值问题的目标是产生一个新的序列 $\hat{X}$ ,预测原序列中不可见的缺失值 $(1-M)\bigodot$ 。
在以上定义的基础上,时间序列预测问题可以视为特殊的时间插值问题:所有的缺失值都集中在序列的后段部分(且连续)。使用形式化描述即对于某个时间步 $\tau$,有 $M[0:\tau]=1,M[\tau:T]=0$ 。
定义 $X,\tilde{X},\hat{X}, Y$ 分别表示不完整目标、完整目标、生成目标与检索到的相关时间序列的随机变量,对应的图模型如下所示:
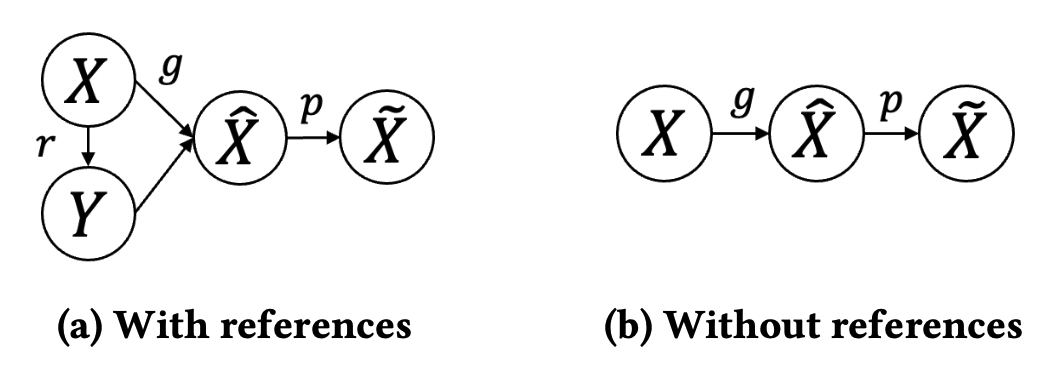
其中$g,r$分别表示生成模型与检索模型,而$p$表示生成序列$\hat{X}$与目标序列$\tilde{X}$之间的关系:假设两者间存在高斯噪声,$p$又可以表示为:
其中$\sigma$是分布的标准差,而$I\in R^{v\times v}$是一个对角矩阵。
使用熵来表征这两个分布间的不确定性 $\Delta=H(\tilde{X}|\hat{X})$。而$\Delta$只与标准差$\sigma^2$有关,等价于MSE的变种(论文中有更加详细的逐步证明),因此我们得到结论:模型所产生的时序结果 $\tilde{X}$ 与目标真实结果 $\hat{X}$ 之间的不确定性等价于他们之间的均方误差MSE。
在此基础上,加入一个相似的检索结果$Y$会对这个误差产生什么影响呢?直觉上,我们当然认为在给定一个相似的序列(集合)后,对于模型的预测会起到一个正面的影响,而作者为了量化其中的关系,继续进行了以下两个方面的论证:
- 上文已知两个序列间的不确定性等价于两者的均方误差。我们想要最小化预测的结果与真实结果之间的均方误差,实际又等价于最大化这两个序列的互信息$I(\tilde{X}; \hat{X})$;
- 对于一个不完全序列$X$,具有以下的互信息大小关系:
最终得到预期的结论:在给定一个或一组相似的时间序列后,其互信息更大,因此模型会更加容易泛化到目标序列。
ReTime算法
在进行严谨的有效性分析后,接下来具体阐述如何通过关系检索获得一组相似的时间序列(Relational Retrieval),以及如何将这一组序列应用到模型的预测中(Content Synthesis),从而获得更加准确的时序预测结果。
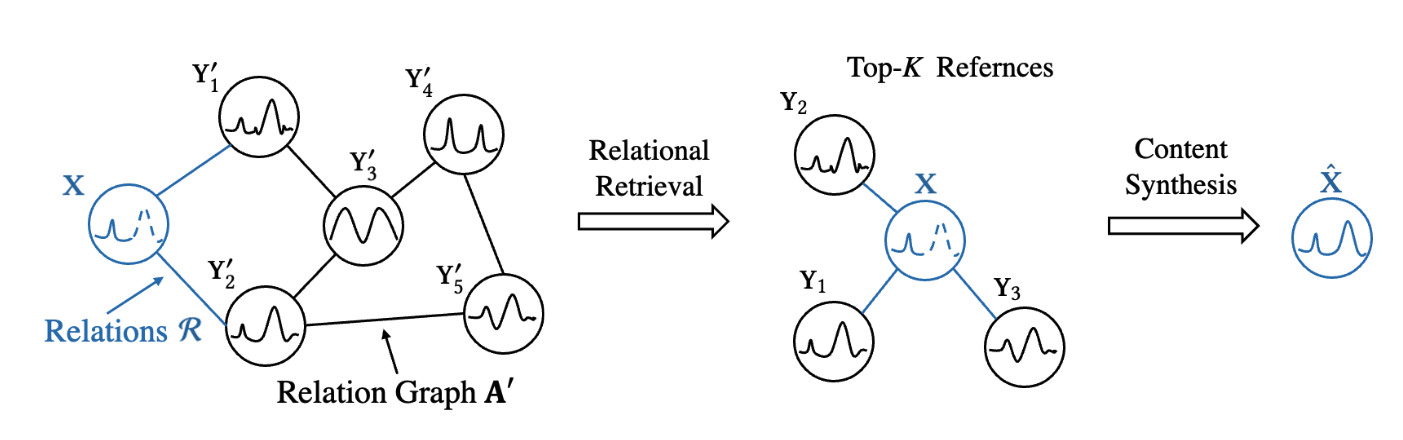
上图是两阶段ReTime算法的步骤,左图表示原图像,其中蓝色圆形表示的是我们想要检索的输入$X$,黑色节点$Y$表示的是用于检索的数据库构成及其邻接关系。在步骤的最开始,根据输入$X$与数据库中节点的相似关系,将其拼接到数据库中;中间的图像表示的是关系检索过程,而最右侧图像表示内容和成过程。
关系检索过程
想要执行该过程,首先需要有两个预备的信息:
- 已知当前查询时间序列与准备的时间序列数据库中数据的相似度关系$R \in N$;
- 已知时间序列数据库中数据间的邻接关系$A’\in R^{N\times N}$。
随后,将$R$拼接到邻接矩阵$A’$的最后一行与最后一列(多出来的对角线元素表征的是节点$X$与自身的相似度,所以直接用1来填充),最终获得完整的邻接矩阵$A\in R^{(N+1)\times (N+1)}$,我们在该邻接矩阵所对应的图中进行随机游走(Random Walk with Restart, RWR),来获得与时间序列样本$X$的近似得分。对应的解析解为:
其中$p$是我们最终想要的与$X$样本的相似度得分,从中取出最大的$K$个,对应的下标查询到的数据库内的节点,就是我们想要获得的用于参照的时间序列。
值得注意的是,这里的检索是纯粹基于时间序列之间的关系进行的检索,而未使用序列之间的相似性之类的指标进行检索。作者解释使用关系检索的原因是在极端的输入数据很短,而预测数据很长的情况下,通过相似度检索获得的子序列可能会非常不稳定。
内容合成过程
在获得了$K$个与当前查询的时间序列$X$最相似的序列后,需要根据得到的参考节点信息,将内容进行合成 —— 显而易见,一个简单的合成方式是把所有参考节点的值取个平均,但作者认为这样会有问题,例如查询序列与参考序列的波峰波谷可能不同,后者也可能存在噪声。所以作者使用了一个NN模型来将参考节点信息合成。
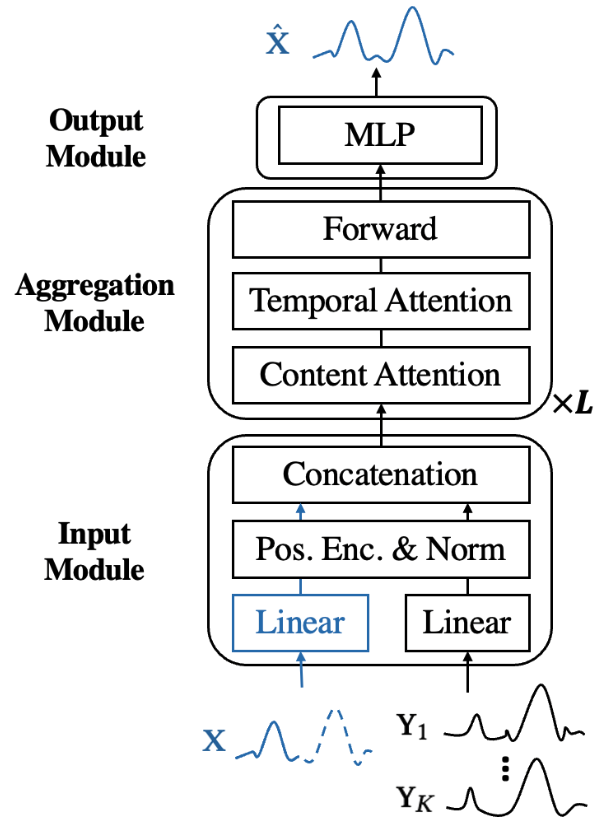
上图是用于内容合成的模型结构,由三个部件构成:
- 输入模块:使用一个线性全连接将序列的已知内容转换成embedding;在此基础上加入位置信息(positional encoding),并将结果进行归一化,最后将结果纵向拼接;
- 聚合模块:在输入模块输出结果的基础上,分别在隐向量维度与时间步维度进行multi-head attention,并通过一个前馈网络;
- 输出模块:通过一个全连接将最终的输出隐向量转换成时间序列的结果。
实验
论文在两个真实数据集上检验了所提出算法ReTime的有效性:
- Traffic:含有每小时的道路平均速度与拥挤程度数据,采集于2000个道路传感器。在该数据集上的邻接关系体现在传感器所在的道路是否邻接。
- Temperature:包含了月度温度数据,从北美$30\times 30$个地区采集的从2001年到2015年的数据。其邻接关系体现在区域是否邻接。
对于这两个数据集,作者分别在时间序列预测与时间序列插值两个领域同时进行了评估,所采用的指标为RMSE。论文所比较的基线模型为N-BEATS、Informer、BRITS和E2GAN(作者也在文中提出了时空维度下的ReTime应用方法及其比较基线模型,在此不过多展开)。
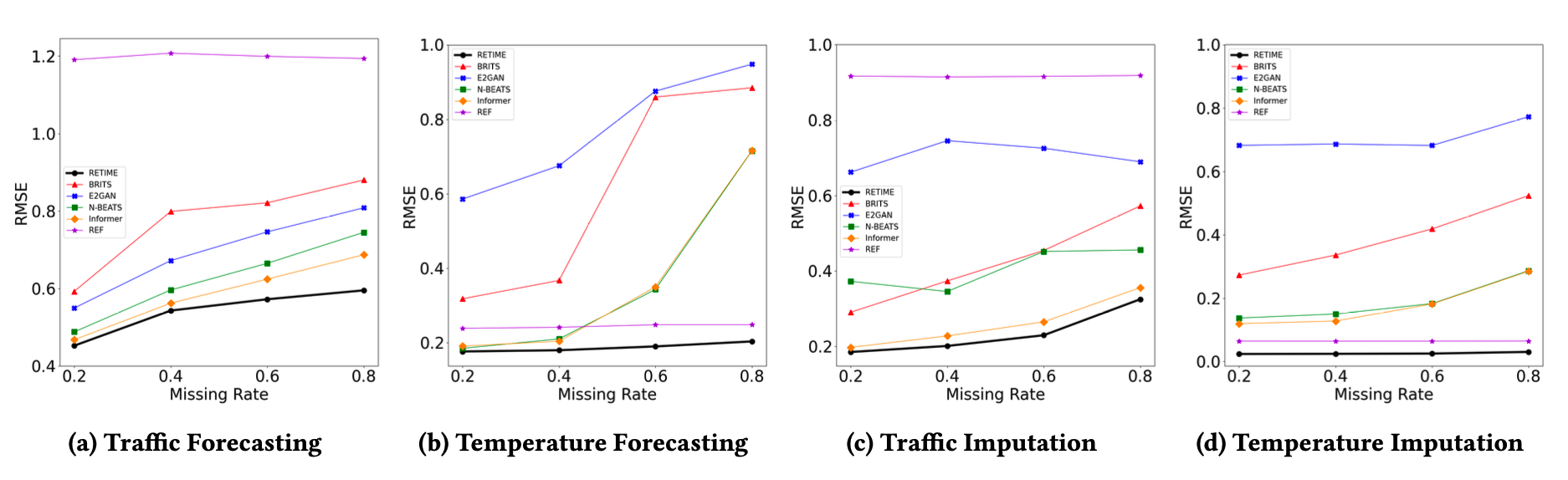
上图为ReTime在两个数据集、两个不同设定下的最终RMSE值,可以看到论文提出的方法在不同设定下都具有很好的效果,超过了所有的基线模型。此外,当missing rate增加,即时序模型可见的数据减少、要预测的序列长度增加时,ReTime能够保持一个相对稳定的效果,而其它方法会有比较明显的效果下降。
为了进一步了解ReTime不同模块起到的作用,作者在几个方面进行了消融实验:
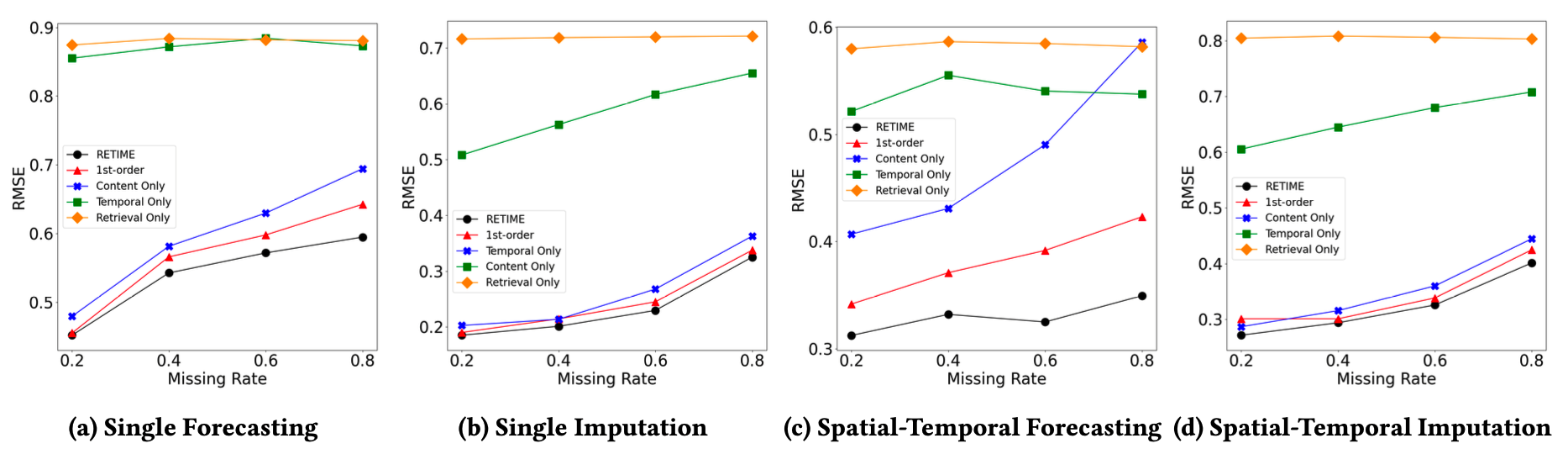
- Temporal/Content Only:在内容聚合过程的模型中,去除某一种注意力聚合机制;
- 1st-order:使用一阶近邻替换随机游走;
- Retrieval Only:不引入内容聚合步骤,只对关系检索后的时间序列值进行平均。
从结果中可以发现,所有的模块都给ReTime方法带来了比较显著的准确度提升。
值得注意的是,其中的结果显示出,如果不进行基于神经网络的内容聚合步骤,直接将检索得到的序列取平均,其结果会非常差,而基于时序的注意力机制起了相对第二大的作用。从直觉上,这是由于作者在检索参照序列的时候,只使用了邻接关系,而没有使用序列模式的相似度关系,所以即使检索到了邻接的节点,也不代表他们的模式是相似的,或者即使他们相似,也不是严格按照时间步对齐的相似。例如:对于traffic数据集,临近的传感器所记录的平均速度、拥挤程度,肯定是有先后关系,代表此处的车流流向了另一处;对于Temperature数据集也有相似关系(时区、海拔不同)。
进一步的讨论
通读完整篇论文,我们会发现:论文对于数据的要求很高,包括但不限于:预先准备一个时间序列数据库,且我们预先知道该数据库里的数据之间的邻接关系(文中的$A’$);我们需要知道当前查询的数据和他们之间的相似关系(文中的$R$,此处隐式地要求了输入的查询数据与数据库中的所有数据必须同构);此外,其实作者在论文中指出,要求数据库中存在的数据量$N$远大于我们想要抽取的相似子集数量$K$,以及要求数据库中的时间序列的长度$T’$远大于查询的时间序列长度$T$;最后 —— 内容合成步骤中的MLP这种编码方式,隐式要求所有输入必须定长 —— 以上种种无疑都给该方法的正常应用打上了一个问号。
从直觉上来说,工业界的数据不会满足这样严格的约束。想象这样一个场景:笔者经营着一个网店,卖不同款式的衣服;现在笔者想对衣服的销量进行预测,了解某款衣服的未来销量如何,其大致走势会是什么样的。特别的,笔者在店铺里上新了某个款式的衣服,这个衣服没有历史的销量,或者只有过去几天的销量,如何预测这款衣服的销量情况呢?
上述场景复现了论文里的所有问题背景:有个销量数据库(已经销售了一段时间的衣服),有个查询样本(新上架的衣服);但又恰好不满足文中所提出的约束条件:作为被查询的数据库,网店中已经在售卖的不同衣服之间不存在邻接关系,作者新上架的衣服与前者也不存在邻接关系。但显然,已有的销量数据对于新上架的衣服是能提供参考的。
怎么解决这个问题呢?直觉上,可以通过衣服是否相似来构造邻接矩阵,而相似性又可以根据不同纬度进行考虑,例如:上架时间、款式(上身下身)、材料、目标人群等等。这是一个比较大的预备工程,而在工作完成之后,我们就能够复原出文中方法所需要的邻接矩阵$A$与关系向量$R$。此外,对于内容合成模型中的定长约束,我们也需要进行等价替代,将MLP替换成一个RNN,或者训练时引入mask等机制,来允许模型能够聚合不定长的数据。