Attention Is All You Need
1. 预备知识
1.1 Encoder/Decoder
序列模型由Encoder与Decoder两部分构成,简单来说,Encoder对input进行编码,而Decoder对编码结果进行解码,解码的结果就是整个序列模型的输出。借用Andrew Ng课件中的截图来进行说明:
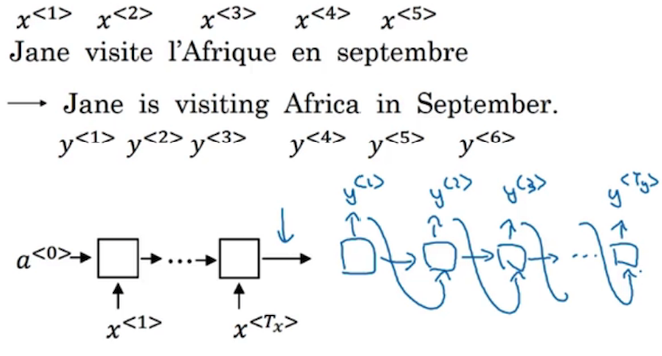
Encoder的每一个单元会根据前一个hidden state以及当前的input来计算当前的hidden state,并将其传到下一个单元中去。而Decoder对于传入的单元进行解码,来找到最合适的一个输出。注意每个Decoder单元只会输出一个output symbol。
以machine translation问题为例给出具体说明。machine translation问题其实是在寻找一个条件概率,在给定输入x(待翻译句子)的前提下寻找结果概率最大,作为输出的翻译结果,具体步骤可以描述如下:
- Decoder的第一个单元对于Encoder部分输出的最后一个hidden state(我们把它记为$h^0$),在候选词表中找一个词A,使得$P(A|x)$在整个词汇表中最大。
- 在第二个单元中,使用$h^1$以及第一单元的输出A作为输入,我们继续找一个单词使$P(A, B|x)$最大,由于$P(A, B|x)=P(B|A, X)P(A|X)$,我们又在第一单元中记录了$P(A|X)$大小,实际上就是对每个单词B,计算$P(B|A, X)$,然后使得$P(B|A, X)P(A|X)$最大即可。
- 同理,一直向下逐个搜索单词,直到出现所有的词输出Prob都不如当前的Prob,就加入EOS并输出。
1.2 Beam Search
有了序列模型的基础,Beam Search实际上就是序列模型选择输出哪一个symbol的方式。
正常来说,我们只需要按照上面的算法不停的算最大概率,每次选择最好的输出就可以了,但是实际上,如果待翻译的语法表中有1000个单词,待翻译的句子长度是10,那么可能的句子构成数量就是$1000^{10}$个。所以直接的全局搜索是不可取的,我们需要找一个能获得近似最优解的词序列,但是又要有能够接受的时间复杂度,Beam Search(集束搜索)应运而生。
集束搜索和贪心其实有一定的相似之处:如果我们选择贪心算法来解这个问题,在搜索最优词时只考虑概率最大的一个候选单词,我们很有可能错过最优解以及很多很好的解。而Beam Search有一个参数 beam width ,也就是每次选择的概率最大的候选单词数,每次使用前面选定的单词组继续向后扩展一个单词,再从其中所有的概率里挑出最有可能的top n。
由于每次算得的Prob都很小,当输出序列比较长的时候,就会出现数值下溢的问题(这也会导致了beam search倾向于寻找更短的答案)。为了解决这个问题,我们要使用 Length Normalization :将目标函数改为Prob的对数和,而不是取Prob的乘积;另外,我们要添加一个正则项,也就是算得对数和之后,我们可以求它的平均值,也就是除以输出的单词数量(在实践中我们通常会使用数量的0.7次方来进行正则)。
我们已经知道,Beam Search的参数有:束宽,单词数的惩罚系数$\alpha$。直观上来说,我们可以知道束宽越大,结果会越好,但是占用的计算时间会更长,内存也会更高。 现在,还有这样一个值得考虑的问题 :如果我们的输出结果不是我们人工所预期的,我们如何知道是RNN——encoder/decoder模型导致了这个结果,还是集束搜索的beam width设置的不够大,没有搜到真正的结果呢?
一个最简单的判断办法是:我们把人工所预期的结果放到RNN模型的decoder中,计算$P(y^*|x)$,如果这个Prob大于模型本身所预测的结果,说明是集束搜索错过了这个更好的结果,而如果Prob要比原来错误结果的Prob更小,那么很显然就是RNN模型出了问题。
1.3 Attention
Attention-中文称注意力机制,这个概念的提出是为了解决:神经网络对记忆长句子的能力较弱,随着待翻译的句子长度增加,其BLEU值将会逐渐下滑这个问题。
我们可以这样来直观的理解Attention机制到底是什么:Attention将决定模型在输出第$t$个output symbol时,how much attention should be paid to t'th input symbol。Attention的具体计算思路如下:
对于每个input symbol,使用一个双向RNN(GRU/LSTM, usually LSTM)来提取每个symbol的特征。因为RNN是双向的,所以第$t$个input symbol的特征$a^t$将由前面传来的$\overrightarrow{a}^t$与后面传来的$\overleftarrow{a}^t$共同决定(Andrew Ng的课件中没有说怎么通过后两者来计算$a^t$,个人觉得就是简单的sum或者concatenate吧)。为了方便表述,我们记$a^t=<\overrightarrow{a}^t,\overleftarrow{a}^t>$
这样,每个input symbol都会有一个描述它自身的特征向量$a^t$。类比于一个全连接层,我们同样将特征向量映射到所有的Decoder单元中,其中第$t^*$个待翻译单词到第$t$个翻译后的输出单词的连接对应的权重为$\alpha^{< t^*, t>}$,而所有连接到第$t$个单词的待翻译单词加权和共同构成了上下文$C$对于这个输出单词的权重,在此记作$C^t$。同样使用Andrew Ng的课件截图来对这个过程进行总结 我似乎已经暴露了这些东西都是在Andrew Ng教授的课件中学的了?
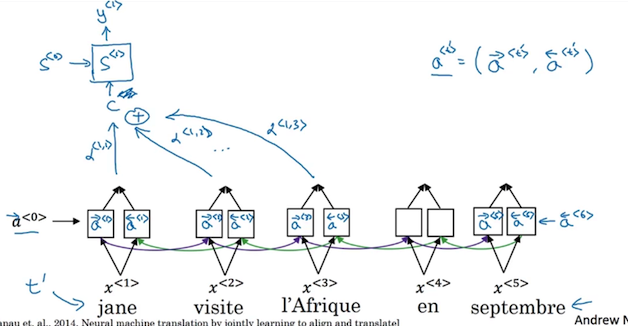
现在的问题转变成了:我们如何确定第$t^*$个待翻译单词到第$t$个翻译后的输出单词的连接对应的权重值$\alpha^{< t^*, t>}$呢?
以第一个output symbol为例,需要计算所有input symbol到它的attention加权之和,我们依次把n个input对于第一个output的权值标记为$\alpha^{< 1, 1>}, \alpha^{< 1, 2>}, …, \alpha^{< 1, n>}$,我们有以下两个要求:
- 所有的权值和为1,也就是要有归一化。
- 因为计算第i个input权值时,我们只知道第i-1个hidden state: $h^{i-1}$与$\alpha^{<1,i-1>}$,所以直观地,应该有$\alpha^{<1,i>}=f(h^{i-1}, \alpha^{<1,i-1>})$。
第一个条件很好满足,假设我们已经计算出了每个input对应的权重,对它使用softmax就可以使所有的权值和为1。
要满足第二个条件其实也比较简单:我们训练一个单层的简单网络,这个网络的输入是$a^t=<\overrightarrow{a}^t,\overleftarrow{a}^t>$与input symbol$_t$,输出是$e<1,t>$,也就是第t个input symbol对于待翻译词的权重 没错,权重就这么被训练出来了 。但是Andrew课件中并没有说这个监督学习的训练对怎么出来,难道是要人工标注?还是涉及到了什么我没有学过所以显得深不可测的知识?
总之,这样我们就可以计算整个上下文对于某个输出的影响了,从概念上来理解,就相当于每个输出在学习前一个hidden state与前一个输出的前提下,又学习了整个上下文与它的关系,因为上下文中每个symbol和它的权值都不同,所以某些和它关系比较大的symbol权重就会大,也就是我们常理解的output symbol pay attention to input symbol了。OVER。
2. Attention Is All You Need
2.1 软广
先推荐一个理解论文时候发现的很有意思的博客:jalammar大神对transformer的图形化解释。这个博客会用很生动的例子与大量动图来解释一些模型,讲的很透彻也很浅显易懂,就是更新慢了点。
下面关于模型讲解的内容中,有相当的一部分来自于这个博客。
2.2 Transformer
我们先来从宏观角度来看,Google Brain的大牛们提出了什么样的一个模型。在我看来,其主要特性是这样的:
- 你们看,我们真的没有用任何CNN和RNN模型哦!(指着Transformer)
- 我们真的没有……偷偷加入multi-head
真香😋 - 我们真的……偷偷加入position encoding
真香😋
好了,认真来说,论文的模型最重要的特性就是完全没有用到RNN/CNN模型。但是不代表模型完全没有使用到这两个模型的思维模式:CNN对特征的高维抽取,在Transformer中用multi-head attention里面的多个产生Query/Key/Value的矩阵替代了,而RNN模型中对序列进行建模的特点,也在Transformer中使用了position encoding来进行变相的替代。我个人挺惊讶于这种把一堆vector用做sum了之后的最终vector放到模型里面跑最终真的非常work的这个结果,可能是大牛们对这些特征的捕捉真的非常到位吧。可以说是非常佩服了。
还有一个很有意思的地方:大牛们对attention这个机制从另一个层面做了解读。上面我们已经说了,attention其实就是在给出输出时,该输出需要参照多少信息在某个input symbol中,而🐂们的理解方式是:我目前要输出的output symbol是一个 query ,而每个input symbol是一个 key ,这个key有对应的 value ,也就是上面所提到的,这个input symbol被双向RNN提取出来的特征。当前output对所有input symbol进行attention的过程,就好比是 用这个query来对所有的key进行模糊查询,获得这个key的value 。模糊查询有多模糊呢,就是每个input symbol对于当前output的权重啦。上面已经说到,这个权重是训练之后使用softmax归一得到的。
希望你也觉得上面的东西很有意思😄 接下来对模型结构进行详细说明。
2.2.1 Encoding/Decoding模块
整个Transformer模型 就是一个Encoder与一个Decoder ,还是以machine translation为例:首先把句子输入到Encoder中,这个Encoder会使用self-attention(简单起见,可以把论文里的scaled dot-product attention/multi-head attention都先看成self-attention)来计算每个input symbol的输出,然后弄成一个vector(因为一个input symbol会产生多个输出——当然不是对所有的vector进行concatenate这么简单,后面 可能 会进行说明)。然后把它们喂给一个前向传播网络,如是反复。Encoder的最终输出结果被转换成两个矩阵K与V,分别对应Key与Value。
Decoder从零向量开始逐个产生output symbol的输出,首先对output sequence同样进行self-attention,不过这次有一个改变的地方,论文中称此为 Masked Multi-Head Attention ,在前面的attention过程中,每个query是知道所有的key的信息做加权的,然而在输出的过程中,对应位置的query只能知道它及之前的位置信息,确保对位置i的预测只能依赖小于i的位置处的已知输出。
2.2.2 Scaled Dot-Product Attention/Multi-Head Attention
在上面,我们知道了什么是attention,实际上是对input symbol的特征进行加权,然后输入到Decoder单元中。在Transformer中进行的处理是类似的,其中使用了一个叫 self-attention 的attention方法,顾名思义,就是自己对自己进行attention,比如有个句子:
The animal didn’t cross the street because it was too tired
在Encoder模块中,这个句子中的每个word,都会与其它所有词进行attention,这个attention连接的权重,或者说Query与Key的模糊匹配程度,揭示了两个词之间的相关程度。比如,可能对词 it 进行self-attention时,发现 animal 与它的连接权重很大,就能一定程度上揭示这个代词指代的是animal啦 因为作为一个没用的模型,我一开始是不知道这个it是指代animal还是street的呀 。
具体来看怎么进行self-attention。如下图所示,比如现在有一个词 Thinking ,已经对它做了embedding,它是一个$d=512$维的向量$X_1$。我们首先把它变成一个 查询-Query 。虽然说是query,其实它还是一个vector,那么怎么把它变成query呢,我们把它乘以一个转换矩阵$W^Q$,这样它就由$X_1$变成了$q_1$。
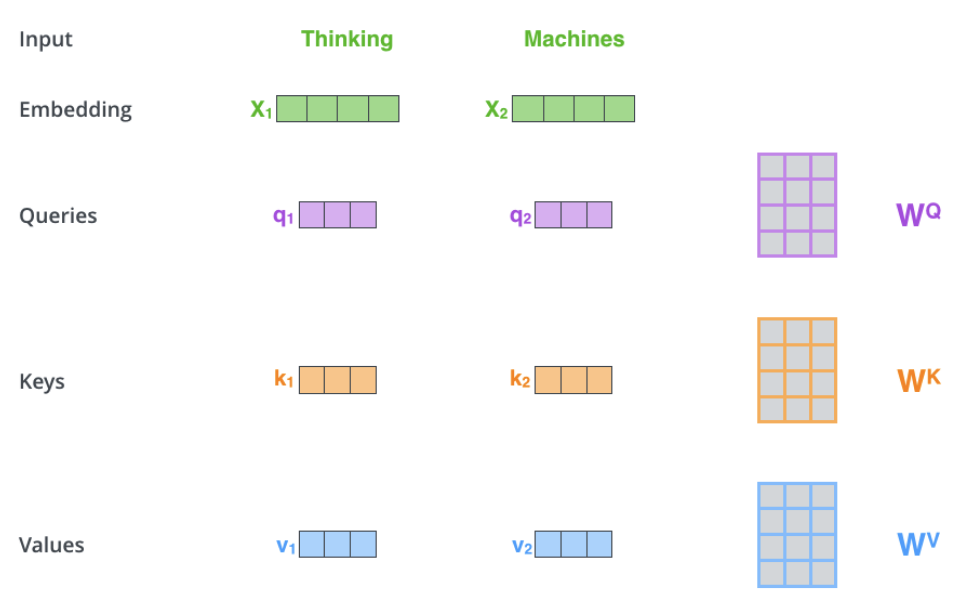
同样的道理,我们把它乘以转换$W^K$,把它变成一个 Key ,把它乘以转换矩阵$W^V$,把它变成一个 Value。这么一看,$X_1$的作用其实很大,所有的一切都是由它自己延伸出来的——这么说对$W^Q,W^K,W^V$矩阵三兄弟就太不公平了,它们仨承担了转换$X_1$的主要责任,它们是怎么来的呢? 它们是在训练过程中训练出来的 。我其实很好奇它们是怎么训练出来的,毕竟论文里面没有详细说。
现在我们有了 queries, keys, values ,剩下的就很简单了,我们求$q_1$与所有的$k$的点积,然后用softmax归一,这就是self-attention中其它词对thinking这个词的权重。对应的value乘以对应的weight,然后加权就是 X1所获得的上下文信息C 。
知道了什么是self-attention,现在可以很简单的解释标题中的两个attention到底是什么了:
- Scaled Dot-Product Attention:实际就是上面所说的加权的整个过程,Dot-Product意为点积,就是指Queries与Keys做点积;Scaled是指在工程实践中,发现在较大的维度情况下,点积会大幅度增大,由此softmax容易陷入局部极小,所以要除以维度的开方,即$\sqrt{d_k}$,这就是scaled词的由来了。这个attention与self-attention的差别仅在于
在softmax之前使用key的维度进行了scale。 - Multi-Head Attention:1中的Attention我们做一次是不够的,可能挖不出来词与词之间的关联关系(或者说挖不完全?),所以上面的$W^Q,W^K,W^V$,我们要生成多个(论文中使用的是8个),这样一个word就会输出多个vector了——可是我们最终是要一个word只有一个vector呀,没关系,我们先把所有的输出concatenate起来,最后再使用一个转换矩阵$W^O$把它转换到正常的维度,这样我们就在多个层次度量了词与词之间的语义关系,并且最终变成了我们想要的输出,这就是命名为Multi-Head的原因。那么你可能又要问了,这个$W^O$又是怎么来的呢,没错,
它又是训练出来的,而且我又不知道它具体是怎么训练的,可以说是非常伤心了。
2.2.3 Position Encoding
如果对RNN稍有了解你可能会发现,上面的所有Attention过程都是对词与词之间进行关联的计算,我们如果直接把上面的结果放进去跑,似乎错过了一个很重要的信息:序列的顺序。
所以呢, 在进行attention之前,也就是刚做完Word Embedding的时候,我们要在Embedding中加入每个词的位置信息 。
👆上面就是论文中给出的获得Position Embedding的方法。我们把这个Embedding加上最开始获得的词向量,就是最开始的input embedding了。
2.3 模型结构概括
简单总结一下Transformer的工作流程:
- 首先计算每个词的embedding,这是一切的基础。
- 在输入一句话时,每个词都有自己存在的顺序下标,使用2.2.3中描述的公式进行这句话每个词的Position Encoding,并加到1中算得的embedding中去。这一步要在输入数据的时候执行,因为只有一句话给出的时候,我们才能知道每个词在这句话的什么位置。
接下来进入Encode步骤 - 使用Multi-Head Attention计算每个词关于其他词的关联关系,并合成一个最终向量(使用2.2.2中说的$W^O$),最终输出的一句话中,每个词都会是一个vector。
因为这个过程中,对每一个word的处理都是独立的,所以可以并行化执行。这是Transformer极其重要的优势之一。 - 把3中输出的一句话中的所有vector送到一个前馈全连接网络,网络的参数在训练中确定,继续输出所有变换后的vector。
- Encoder中重复了3、4两个步骤一共6次,最顶层的Encoder单元将输出的vectors转换成
这里没有说怎么转换的矩阵K与V。这两个矩阵是用来计算Encoder-Decoder Attention的。接下来进入Decode步骤 - 在Decoder的第一个sublayer中,对输入的output向量做Multi-Head Attention,原理同2.2.2。
- 第一个sublayer的输出对K/V矩阵再做一次Encoder-Decoder Attenion:使用输出vector用K/V矩阵计算加权。这是第二个sublayer。
- 第三个sublayer中,使用前馈全连接网络对vector进行变换。
- Decoder中重复了6、7、8三个步骤一共6次,最顶层的Decoder单元每次会输出一个vector,使用一个简单的全连接网络把这个向量映射到整个输出空间vocabulary表中,来获得每个vocabulary的概率,并使用Softmax进行归一。
- 选择9中概率最大的word作为本次Decoder的输出单词。
- 重复9、10两步直到最后一个输出的word是特殊字符:EOS,表示一个字符串的结束。