Kick Start 2018-Practice Round

发表时间 | 分类

Google的Competitions with Google上有三个类型的练习：

  • Hash Code: 应该是一个组队编程训练，看起来比较偏工程向，介绍中说可以选择队伍与编程语言来完成一个engineering problem，还问了一句Are u up for the challenge? Of course I am not.
  • Code Jam: 编程果酱？？ 反正就是用多轮的算法问题来进行比赛，最后获胜者还有奖金，又问了一句Do u have what it takes? emmmm..
  • Kick Start: 今天的重头戏，介绍中说主要是磨炼自己的coding水平，受众是学生 我 和新接触编程的人 我 ，也是按轮次进行的，可以只参加一轮也可以全部参加，最后的问题是What are u waiting for? 这看起来就正常多了，不像是向一个算法渣挑衅的言论，给好评。

Kick Start的轮次是一个Practice Round和A~H八轮，其中除了Practice Round给了24h解题外，其它的八个轮次都是只给3h解题时间，所以介绍中所说的’可以只参加一轮’，实则是指哪一轮呢？

别问，问就是自闭。

Quick-Start Guide

在开始解题之前，还要学习怎么使用Kick Start平台。本来不想写这部分的，后来粗粗看了看，发现解题形式和我之前常用的POJ或Leetcode 其实我不常用，但是常用一词会显得我在这方面非常qualified 差别还是不小的，所以来这里整理一下：

  1. 如果想参加的是比赛，要在contest’s home page（当然还要在比赛举行时间）进行解题，如果是练习就滚去Past Problems，选择自己想自闭的轮次

  2. 要注意limits模块中的内容，因为很多时候不是WA，而是TLE，就像最难过的事情不是我不行，而是我本可以。

  3. 下载问题文件之后，需要生成result文件并提交。在practice中只需要提交result文件，在competition中还需要提交code文件。提交结果有三种：
    A. Correct
    B. Rejected：就是提交被并非对错的原因被否决了，比如传错了文件
    C. Incorrect：回答错误

  4. 比较有意思的是，Kick Start中的设定是，先写自己的程序，写完觉得没问题了点击下载数据集，一开始只能下载Small规模的数据集，从下载后开始计时，小问题是4分钟，解答正确后才能下载大数据集，大问题是8分钟。需要在指定时间内提交答案，如果提交答案正确，结束计时；如果提交Rejected，计时会继续走，还能继续提交；如果提交答案错误，会被计一次罚时，值得注意的是，如果计时结束也没有提交或者还是Rejected，也会自动判为Incorrect，此时已经没有提交机会了。

  5. 大数据集评分只有在比赛结束后才能看到，也就是说，提交之后是看不到自己的结果的。对于大数据集，只会judge最后一次上传的结果，可以在8分钟限时内反复提交。

  6. 当然，以上所有的限制在Practice mode下不会生效，这是给自闭儿童的一大福利。

关于读取input.file并输出output.file

对于C++

在solution.cpp中编写解决问题的代码，输入输出使用cin与cout即可，在编译时使用以下命令：

1
2
g++ solution.cpp -o solution
./solution < input_file.txt > output_file.txt

第一步是为了生成名为solution的可执行文件，当然如果嫌麻烦直接省去-o参数，直接生成a.out也行。

第二步是运行这个可执行文件，并指定输入文件名为input_file.txt，输出到output_file.txt中。

对于Python

使用raw_input()函数读取，使用print输出以及format方法控制格式即可。在执行时输入以下指令：

1
python2 solution.py input_file.txt output_file.txt

Python的执行语句就非常的简单粗暴了。通过以上的例子可以发现，实际编写代码时和平时其它平台上的输入输出相比几乎没有区别，只是在执行代码时添加了条件。

Problem A. GBus count

问题描述

这道题算是签到题吧，忽略输入输出的格式要求，题目内容是这样的：

存在一些城市，从1开始向后编号。现在有$N$辆公交车，其中第$i$辆公交从城市编号$A_i$开往$B_i$（前后都能取到），那么现在问城市$j$有几辆公交车可以到达。

拍脑袋：Brute Force

最容易想到的解法是这样的：

开辟一个数组，表示每个城市有几辆公交可以到达，城市有多少我数组就开多大。数组的值初始化为0。
每读入一个数据，比如第$5$辆公交车从$10$开往$15$，那就把下标是$10$到$15$的数组中的数字全部增加1。
对所有的公交车都处理完毕之后，能到达第$i$座城市的公交车数量，就是数组中下标为$i$元素的值。

啊，好简单，然后写了代码，测试了一下，居然还过了。 这是我个人的一小步，是Brute Force掌控世界的一大步

small case

large case

然而如果不欺骗自己的话，就能想到这个办法是很愚蠢的。因为我不想一一列举这个方法有多愚蠢就像我不想证明自己很愚蠢一样，所以我只是说明一下结果，这个方法会因为城市数的增加以及一些不好的数据（比如所有公交车能到达的两个城市都隔得很远）等情况，导致时间复杂度太高而解不出题目来。

我大概能明白因为这是Practice轮次的题又是第一题，所以Googler并不想为难我们，但是还是要认真思考一下怎么做。

线段树？

我深知学习的过程就是一个不断递归的过程，就好比我要用线段树求解这道题，我就要先把这篇博文压栈，跑去学什么是线段树，然后写一篇重修数据结构：线段树，写完以后再恢复这篇文章的环境，继续开始写一样。如果我在学习线段树的过程中又出现问题，那我就要二次压栈，就像生活把重担一次又一次压在我的肩头。

为什么会想到用线段树来做这道题呢？其实我也不知道……因为如我在线段树博文中所说的，这道题其实是不满足局部影响全局的特性的。如果要找到一个影响全局的值，那可以设置为：经过这个区间的公交的总数(sum)，但是最后查询却不是一个区间，而是一个确定的值——那数组的查询效率是$O(1)$啊！线段树反而要花费$O(\mathrm{log}n)$的时间，为什么要看不起数组呢？

因为我查了网上的解题资料，ACPC的大神们都是用线段树解题的。我和大神的思路差距实在是相去甚远啊，拜服。

大概看了一下大神的代码，就是说使用线段树来存储区间的更新，然后在查询的时候把更新的结果一路向下带到叶子节点中去（是否要向下带要看设置的标志位，向下带之后修改标志位即可）。那么这个解法的时间复杂度是多少呢，如果城市有$m$座，公交车有$n$辆，查询的次数是$k$次。

大神把线段树保存在数组中，数组的下标对应于树的结点编号，也就是说$i$的父节点编号是$i<<1$，子节点编号是$i>>1,i>>1|1$，节省了存储空间（权且作为一个trick吧）

构建线段树的时间复杂度是$O(m)$，根据公交车区间来更新这棵线段树的时间复杂度是$O(n\mathrm{log}m)$，最后查询的时间复杂度是$O(k\mathrm{log}m)$。所以总时间复杂度是$\mathrm{max}(O(m), O(n\mathrm{log}m), O(k\mathrm{log}m))$。

黑人问号.jpg

看到这里的时候我是有点懵逼的，这看起来查询的时间复杂度反而比所谓的数组中的常数时间复杂度要高啊？

花开两朵，各表一枝。另外我查到了一个感觉很棒的思路，就是我们其实不需要存储每个城市到底有几辆公交车会经过，我们也可以在每次查询时遍历整个公交车经过的区间，看看有多少个区间包含了这座城市就行了。和Brute Force比较呢，我们还是考虑城市有$m$座，公交车有$n$辆，查询的次数是$k$次，那么前者的复杂度是$\mathrm{max}(O(mn), O(k))$，后者的复杂度是$O(nk)$，这样我们就可以根据$m,n,k$的不同规模来考虑使用不同的解法了。

总结

所以我们来总结一下上面提到的三种解法：

  • Brute Force: $\mathrm{max}(O(mn), O(k))$
  • 查询时搜索：$O(nk)$
  • 线段树：$\mathrm{max}(O(m), O(n\mathrm{log}m), O(k\mathrm{log}m))$

可以看到，这道题的解法是比较多样的，但是没有绝对意义上优秀的解法。Googler把这道题的test case规模设置的只要是个解就能过，所以就不进行过多的讨论了。

哦对了，所有的程序我都放在最后了，以免影响阅读体验。

Problem B. Googol String

问题描述

现在有一个$0,1$字符构成的字符串序列，定义如下：

$S_0 = “”$
$S_1 = “0”$
$S_2 = “001”$
$S_3 = “0010011”$
…
$S_N = S_{N-1}+”0”+\mathrm{switch}(\mathrm{reverse}(S_{N-1}))$

其中，reverse表示对一个字符串进行反转，switch表示对字符串按位取反
现在要求你找出字符串$S_{\mathrm{googol}}$的第$K$个字符的值是0还是1，其中$\mathrm{googol}=10^{100}$

解题思路

乍一看这么大的串很唬人，其实是可以转化为一个比较简单的找规律问题的但是要想出如何转化成这个找规律的问题很难嘤嘤嘤。首先从题目中可以比较轻松的获得下面这些信息：

  1. 第$S_N$个序列的长度是$S_{N-1}$个序列长度的2倍再加1，相当于是$S_{N-1}$本身+一个字符0+$S_{N-1}$的一个复合变换。
  2. 只要计算出了$S_{N-1}$序列，那么$S_N$序列的前$|S_{N-1}|$个字符一定与$S_{N-1}$相同——因为$S_N$的前$|S_{N-1}|$个字符就是$S_{N-1}$。
  3. 一个序列$S_N$的后一半中的某一个数一定与前一半中的某一个数相关，或者用更加有意思的话来说，叫对称，这个要解释一下：

    假设我们已经知道$S_2=”001”$。现在考虑$S_3$，它的长度是$2\times3+1=7$，其中第$4$个字符是我们用来分隔前后一半的字符，当然，根据序列的构造规则，这个字符一定是”0”。
    现在我们考虑$S_3$中第$6$个字符，这个字符根据构造规律，我们可以找到在$S_2$中的变换成它的那个数字，当然因为$S_2$已经被包含在$S_3$的前3个字符中了，我们直接从$S_3$中来观察它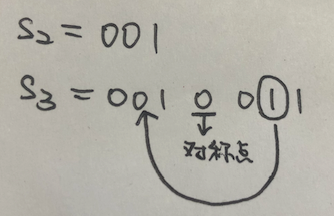
    黑人问号.jpg
    也就是说，第6个字符关于第4个字符（它是在构造$S_3$时连接左右两边字符串的对称点）对称到第2个字符，并且根据构造条件，它是第2个字符的反转，因为第2个字符是0，所以我们可以推知第6个字符是1

    此时我要重述一下以上推导的条件：我们现在已经知道$S_2$，还不知道$S_3$，而我们要求的是：$S_3$的第6个字符是0还是1。我们可以通过把它映射到$S_2$中的第2个字符来得到。上面的图片仅仅是方便说明字符之间的映射关系的，并不是说我们已经知道了$S_3$是个什么序列。

通过上面的推导，我们可以得出这样一个结论：就是不管$S_N$中这个$N$有多大，我要找的第$K$个字符一定与$S_{N-1}$有关，而$S_{N-1}$又与$S_{N-2}$有关……以此类推，其实我们要找的字符串就是$S_1$的一个变换而已。这个递推在编程中可以用递归来实现。

所以我们解题只需要这样做：

  • 对于给我们的一个$K$，我们先找到一个数$N=2^n, n=1,2,…$，这个数小于$K$但离它最近。
  • 我们求$K$关于$N$的对称点位置，把这个位置$K^\prime$作为新的$K$，但是我们要求的$K$的数值其实是$K^\prime$数值相反的，也就是说$\mathrm{value}_K=1-\mathrm{value}_{K^\prime}$。
  • 重复上面两步，直到$K=1$为止，而我们知道$K=1$时$\mathrm{value}_K=0$。

举个🌰：我们现在要求$S_{\mathrm{googol}}$中的第$K=11$个字符是数字0还是数字1：

  1. 我们先找到离它最近的$N=2^n=8$，将11关于8求对称点，那就是5，好，那就是11是5的取反；
  2. 找到离5最近的$N=2^n=4$，将5关于4求对称点，那就是3，那5是3的取反，又因为11是5的取反，取反的取反就是自身，所以$11=3$；
  3. 找到离3最近的$N=2^n=2$，将3关于2求对称点，那就是1，1是3的取反，也就是11的取反。
  4. 我们知道$K=1$是数值0，那么$K=11$就是1，这就是最终结果。

同上，程序放在最后。

Problem C. Sort a scrambled itinerary

问题描述

我们的Mary同学想要乘坐飞机从一个城市到达另外一座城市，但是中间可能会经历零次到多次的转机过程（当然转机是在不同的城市转的，否则没有意义）。

粗心的Mary把所有的机票次序搞混了 让我们忽略为什么Mary不能根据乘坐飞机的时间来对机票进行排序的问题 ，所以现在你看到的是一系列从一座城市到另一座城市的票，要求你排列出正确的飞行顺序，用’A-B’的形式输出。

解题思路

这道题又是比较简单的题，也没有在数据规模上卡什么严苛的解题思路。我是这么考虑的：

因为城市的顺序是以’出发城市-目的城市’对的形式给出的，所以我们收集所有的出发城市集合$S$，与到达的所有城市集合$T$，可以得到一个很有趣的结论： $S$与$T$的并集$A$是所有Mary会经历的城市，但是$S$和$T$与$A$会分别相差一座城市 ，因为$S$中所有的城市是机票中所有的出发城市，所以在$A-S$集合中唯一的一座城市，是我们最终的目的地城市；同理$A-T$集合中唯一的一座城市，是我们要出发的城市。

那接下来就很好做了。我们用一个 字典 类型的结构$\mathrm{s2t}$来存储这个’出发城市-目的城市’对，从出发城市开始依次求：

出发城市$S_0$ $\rightarrow$ 第一座要中转的城市$S_1=\mathrm{s2t}[S_0]$ $\rightarrow$ 第二座要中转的城市$S_2=\mathrm{s2t}[S_1]$ $\rightarrow$ …… $\rightarrow$ 要到达的城市$S_n=\mathrm{s2t}[S_{n-1}]$
循环终结条件是：当我们最后从字典里读出来的城市$S_{n}$是我们的目的地城市。

Problem D. Sums of Sums

问题描述

给定一个长度为$N$的数组，用下面的形式构成一个新的长度为$N\times (N+1)/2$的数组：

  1. 对于原数组，我们分别取其长度为$1,2,…,N$的子串，并对这个子串求和，加入到新的数组中。
  2. 当然易知，新的数组中的元素个数就是$N+(N-1)+…+1=N\times (N+1)/2$。
  3. 对这个数组进行排序，令其从小到大排列。

现在对新数组进行$Q$次区间查询，返回这个区间的元素之和。

解题思路

可以比较清晰的看出，这是一个比较典型的线段树的问题。但是为了不让问题显得太过简单，Googler首先对一开始的元素做了一个变换（但是事实上，这个变换仍然不会占用太高的时间复杂度）。

对于从一个给定数组构建一个新的数组，只需要用一个固定长度的滑动窗口去扫描计算和就可以了。窗口的大小从1开始扩展到$N$，然后用这个窗口滑动整个$N$的长度，所占用的总时间复杂度为$O(N^2)$。

之后我们用这个长度为$N^2$数量级的数组来构建一棵线段树，所需要的时间复杂度为$O(N^2\mathrm{log}N^2$，（在这里没有对线段树的更新，所以可以不写相应的函数），查询的时间复杂度为$O(\mathrm{Qlog}N^2)$。

遇到的坑：千万要把结果类型设成long long int而不是int，不然会返回负数的！血泪教训！

在实际解题时候，对于小规模数据集是能够成功correct的，但是大规模数据集算了十分钟以后因为疯狂吃内存，系统居然自动给我把进程杀了……虽然哪怕不杀掉也已经超出限制时间了。

从网上找了找相关的解题思路，大神们用的应该是树状数组做的： 因为线段树在空间复杂度上是树状数组的两倍 。这也应该是我疯狂爆内存的原因。后面的查询时间复杂度还没有建树高呢，不至于卡半天没出来。

程序们

Problem A. GBus count

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
// 此为Brute Force解法
#include<iostream>
#include<vector>
#include<algorithm>
#include<cstring>
using namespace std;

const int maxn = 5050;

int main(){
    int res[maxn];
    int T, N, P;
    cin>>T;
    for(int i=0;i<T;i++){
        memset(res, 0, sizeof(res));
        cin>>N;
        int a, b;
        for(int j=0;j<N;j++){
            cin>>a>>b;
            for(int k=a;k<=b;k++) res[k]++;
        }
        cin>>P;
        int c;
        vector<int>r;
        for(int j=0;j<P;j++){
            cin>>c;
            r.push_back(res[c]);
        }
        cout<<"Case #"<<i+1<<": ";
        for(int j=0;j<r.size();j++) !j ? cout<<r[j] : cout<<" "<<r[j];
        cout<<endl;
    }
    return 0;
}

Problem B. Googol String

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include<iostream>
#include<vector>
#include<algorithm>
#include<cstring>
using namespace std;

// 当前s_n中要查找的字符k
int recurse(long long k){
	// 如果迭代到最初的起点，返回0
	if(k == 1) return 0;

	// 找到离k最近的能被2整除的数
	long long half = 1;
	while(half <= k) half <<= 1;
	half >>= 1;
	// 如果当前k就在当前这个分割点上，则k肯定是0
	if(half == k) return 0;
	// 否则，将k关于找到的数进行对称翻转，迭代寻找值
	return recurse(2*half-k) ^ 1;
}

int main(){
	int tk;
	cin>>tk;
	for(int i=0;i<tk;i++){
		long long num;
		cin>>num;
		cout<<"Case #"<<i+1<<": "<<recurse(num)<<endl;
	}
	return 0;
}

Problem C. Sort a scrambled itinerary

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
T = int(raw_input())

for time in range(T):
    N = int(raw_input())
    st_pair = dict()
    for _ in range(N):
        source = str(raw_input())
        target = str(raw_input())
        st_pair[source] = target
    sources = st_pair.keys()
    targets = [st_pair[key] for key in st_pair.keys()]
    os = list((set(sources) | set(targets)) - set(targets))[0]
    ot = list((set(sources) | set(targets)) - set(sources))[0]

    sw = os
    print "Case #%d:" % (time+1),
    while st_pair[sw] != ot:
        print "%s-%s" % (sw, st_pair[sw]),
        sw = st_pair[sw]
    print "%s-%s" % (sw, st_pair[sw])

Problem D. Sums of Sums

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
#include<iostream>
#include<vector>
#include<algorithm>
#include<cstring>
using namespace std;

// 线段树
struct SegmentTree{
	long long int start, end;
	long long int sum;
	SegmentTree *left, *right;
	SegmentTree(long long int start, long long int end, long long int sum){
		this->start = start;
		this->end = end;
		this->sum =sum;
		this->left = NULL;
		this->right = NULL;
	}
};

// 构建一棵线段树
SegmentTree* build(long long int start, long long int end, vector<long long int> &nums){
	if(start > end) return NULL;

	// 创建根节点，并进行初始化
	SegmentTree *root = new SegmentTree(start, end, nums[start]);
	if(start == end) return root;

	long long int mid = (start+end) / 2;
	root->left = build(start, mid, nums);
	root->right = build(mid+1, end, nums);
	root->sum = root->left->sum + root->right->sum;
	return root;
}

long long int query(SegmentTree *root, long long int start, long long int end){
	// 如果待查询区间包含当前区间，直接返回数值
	if(root->start >= start && root->end <= end) return root->sum;

	long long int mid = (root->start+root->end) / 2;
	long long int sum = 0;
	if(mid >= start) sum += query(root->left, start, end);
	if(mid+1 <= end) sum += query(root->right, start, end);

	return sum;
}

int main(){
	long long int T, N, Q;
	vector<long long int> origin_nums;
	vector<long long int> nums;
	cin>>T;

	long long int num, sum;
	vector<long long int>res;
	for(long long int i=1;i<=T;i++){
		cin>>N>>Q;
		origin_nums.clear();
		nums.clear();
		res.clear();
		for(long long int j=0;j<N;j++){
			cin>>num;
			origin_nums.push_back(num);
		}

		// 滑动窗口构建新数组
		for(long long int length=1;length<=N;length++){
			long long int last = 0;
			for(long long int j=0;j<length;j++) last += origin_nums[j];
			nums.push_back(last);
			for(long long int j=1;j<=N-length;j++){
				last = last-origin_nums[j-1]+origin_nums[j+length-1];
				nums.push_back(last);
			}
		}

		// 构建线段树
		sort(nums.begin(), nums.end());
		SegmentTree *root = build(0, nums.size()-1, nums);
		// 对线段树执行查询int
		long long int start, end;
		vector<long long int> res;
		for(long long int j=0;j<Q;j++){
			cin>>start>>end;
			res.push_back(query(root, start-1, end-1));
		}
		cout<<"Case #"<<i<<":"<<endl;
		for(auto result:res) cout<<result<<endl;
	}
	return 0;
}