🌲系列的继续~

111. 二叉树的最小深度

要求一棵给定二叉树中，从根节点到叶子节点的最小深度。这个使用递归来求解就可以了。一个可以考虑优化的点是：传入的参数可以从传值改进为引用传递，因为递归(dfs)搜索的时候可以动态修改当前搜索的深度。

给定一棵树和一个数字，判断树中是否存在一条路径，这条路径的结点值之和就是该数字。没啥好说的，同样进行递归搜索，共享一个路径和的参数，搜索到叶子节点的时候判断当前参数是否与目标数字相等。

和上面题相同，唯一的区别在于从判断 是否存在路径和 变成了 找到所有的路径。在传递的参数中加入一个：走到当前节点的路径就可以了。

说是展开为链表，其实是展开成一个 只有右结点的树 ，也就是把所有的节点都放到这个树的右节点上。

同样进行递归：

边界条件：如果树节点为空，直接返回。
否则，递归对树的左右节点进行处理。
把当前节点的左节点链接到右节点上，具体地：
1. 首先找到左节点的最后一个右节点，然后把当前节点的右节点接到后面。
2. 把当前节点的右节点改成它的左节点。
3. 把当前节点的左节点置空。

因为我们已经递归对下面的子树进行了处理，当前左子树一定满足已经展开成’链表’了，所以左子树中只存在右节点，一路向下找找到最后一个是很容易实现的。

难题先搁置

就是在一棵树的struct定义中增加了一个指针TreeNode *next，目的是要把它连接到这个节点的兄弟节点上。注意 要连接到同一层右边的那个节点，哪怕不在同一个父节点上 （当然如果同一层右边已经没有节点了，那就置为NULL）。

116题与117题的区别在于，前者保证了树是完全二叉树，这样的话可以默认 左子节点连接右子节点 ，然后 右子节点连接当前节点右兄弟的左子节点 这样的形式。我们直接考虑117题，也就是可能不是完全二叉树的情况——其实两者难度本来也没差多少。

好了，要进行递归，我们需要形式化的考虑以下的内容：

边界条件：如果树节点为空，直接返回，不需要设置它的next节点
如果树存在左右节点，递归对左右节点进行处理： 注意一定要先处理右节点，再处理左节点！ 。因为先处理左节点的话，右节点的next关系还没有形成，会造成误判。比如下图这种情况：

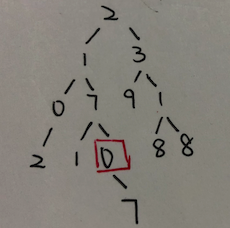
红框内的0在先处理左右子树的情况下是结果是不一样的：
1. 如果先处理左子树，那么此时左子树处理结束后，第三层已经有链接关系$0\rightarrow7\rightarrow9$，但是由于右子树节点还未处理，还没有产生$9\rightarrow1$的节点。这个时候如果想要找0的兄弟节点，我们考察节点7的兄弟节点9，发现就没有子树，这个时候我们照理应该继续考察1，但是由于9到1还没有产生连接，查找已经到底了。这样会导致程序认为第四层的0没有兄弟节点——而实际上它是有兄弟节点8的！
2. 如果先处理右子树，产生链接关系$9\rightarrow1$之后再进行上述搜索，就能够成功搜索到第三层的节点1，从而成功将0连接到8上。
分情况进行：将左节点连接到右结点/将右节点连接到之后的节点/将左节点连接到之后的节点。

118要求给出一个$n$行的杨辉三角，119要求给出第$n$行杨辉三角的值。两者都不难，迭代更新数组即可。其中119还要求最好使用$O(n)$的空间复杂度来解决问题， 使用一个数组对这个数组进行更新 就可以了。

使用vector< vector>形式给出一个三角形，给出三角形自顶向下的最小路径和：迭代更新每一层的最短路径，最后在最后一层搜索最短的那个路径和就可以了；或者我们可以自底向上更新最短路径，然后只取三角形顶端的数字即可。后者的时间常数会更小一点。